Entendendo a Similaridade Vetorial utilizada em Aprendizado de Máquina

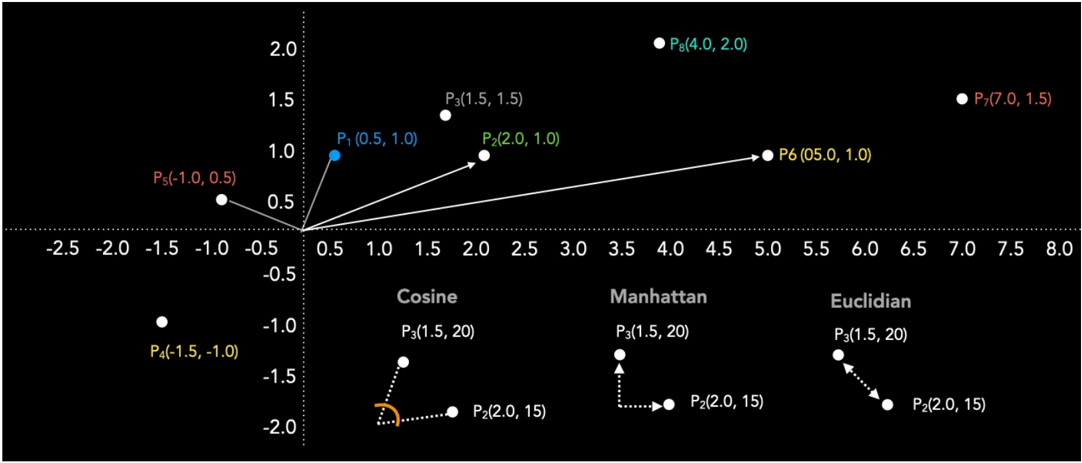
As medidas de similaridade desempenham um papel central em Aprendizado de Máquina, pois quantificam, de maneira matemática, o quanto objetos, pontos de dados ou textos por meio de vetores se assemelham. Compreender o conceito de similaridade no espaço vetorial e escolher a métrica adequada é fundamental para resolver problemas do mundo real, como sistemas de recomendaçãoo ou chatbots baseado em RAG. Existem diferentes formas de calcular a proximidade entre dois vetores em um espaço de vetorial. Por exemplo, o uso de Similaridade de Cosseno, Produto Escalar, Distância de Manhattan (L1) ou Distância Euclidiana (L2).

Produto Escalar

O produto escalar é uma métrica amplamente utilizada para medir similaridade. Ele leva em conta tanto a direção quanto a magnitude dos vetores, considerando se apontam para o mesmo lado e se possuem “tamanhos” parecidos. É indicado quando direção e magnitude são relevantes. O resultado é sempre um escalar, que pode variar de menos infinito a mais infinito: valores negativos indicam direções opostas, valores positivos indicam direções semelhantes e valor zero indica vetores perpendiculares [1]. Quanto maior o valor, mais alinhados e similares os vetores são.

dot_product(a, b) = Σ (aᵢ × bᵢ) = a₁b₁ + a₂b₂ + ... + aₙbₙ

Do ponto de vista geométrico:

dot_product(a, b) = |a| × |b| × cos(θ)

onde |a| e |b| são as normas (ou módulos) de a e b, e θ é o ângulo entre eles.

Similaridade do Cosseno

A similaridade do cosseno considera apenas o ângulo entre os vetores, ignorando a magnitude. Para calculá-la, basta dividir o produto escalar pelo produto das normas de cada vetor, normalizando o valor (que sempre estará entre -1 e 1 — dessa forma, o resultado é invariante ao tamanho dos vetores). Essa métrica é especialmente útil para saber se os vetores “apontam” na mesma direção, sem considerar magnitude.

cosine_similarity(a, b) = dot_product(a, b) / (|a| × |b|)

Exemplo com PyTorch

import torch
import torch.nn.functional as F

# Método 1: Usando F.cosine_similarity
cos_sim_1 = F.cosine_similarity(vector1, vector2)

# Método 2: Cálculo manual
cos_sim_2 = torch.dot(vector1, vector2) / (torch.norm(vector1) * torch.norm(vector2))

Na figura abaixo, é possível ver o cálculo desses valores: ao comparar A = (1.5, 1.5) e B = (2.0, 1.0) em um espaço de embeddings 2D, a similaridade do cosseno é 0.948, indicando alta similaridade direcional. Já comparando A (1.5, 1.5) com C (-1.0, -0.5), o valor é -0.948, mostrando que estão em direções opostas.

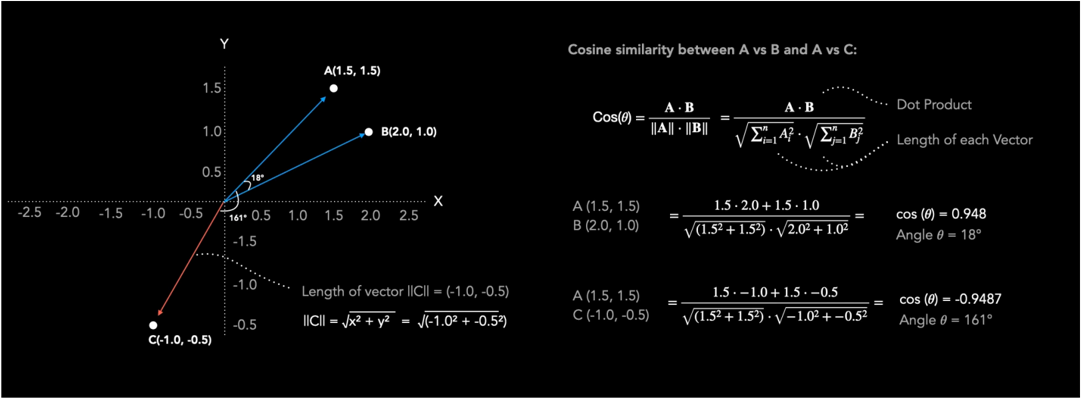
Se o cosseno do ângulo resultar em zero, significa que os vetores são perpendiculares (nem similares, nem dissimilares).

Relação entre Produto Escalar e Similaridade do Cosseno

Os dois conceitos estão diretamente relacionados: o produto escalar corresponde à multiplicação do cosseno do ângulo pelos módulos dos vetores.

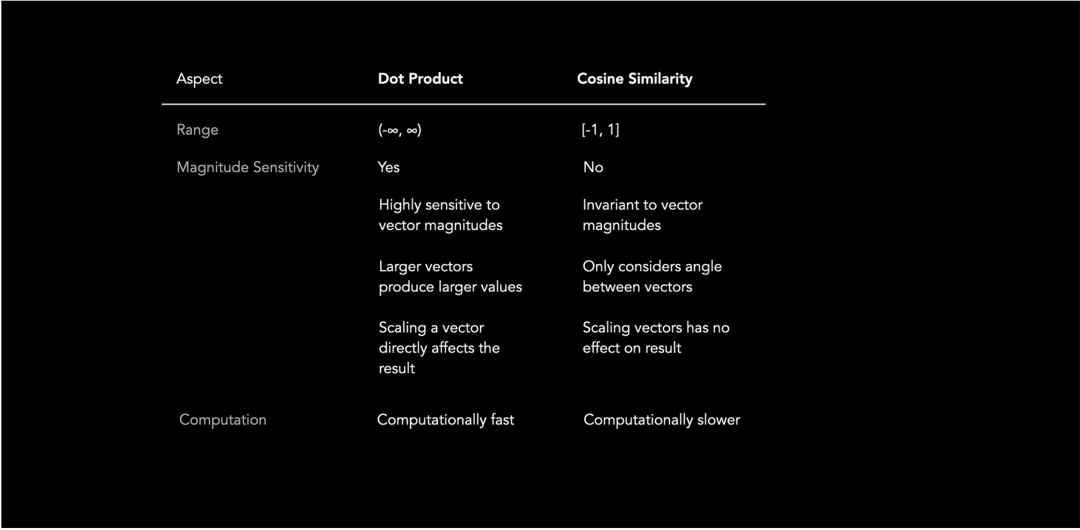
O produto escalar leva em conta tanto a direção quanto o tamanho dos vetores, enquanto a similaridade do cosseno depende apenas da direção. Quando ambos os vetores são normalizados (módulo igual a 1), o produto escalar e a similaridade do cosseno apresentam o mesmo valor.

Aplicação: Frequência de Palavras em Documentos

Considere um exemplo em que comparamos documentos levando em conta apenas a frequência de ocorrência das palavras A, B e C.

• Documento 1: [10, 20, 30]
• Documento 2: [100, 200, 300] (proporcionalmente igual ao Doc 1, mas 10x maior)
• Documento 3: [30, 20, 10] (proporções diferentes)
• Documento 4: [200, 300, 100] (proporções diferentes e valores maiores)

Comparando a similaridade entre documentos tanto pelo produto escalar quanto pelo cosseno:

import numpy as np

def dot_product(vec1, vec2):
    return np.dot(vec1, vec2)

def cosine_similarity(vec1, vec2):
    return np.dot(vec1, vec2) / (np.linalg.norm(vec1) * np.linalg.norm(vec2))

Resultados obtidos:

• Produtos escalares: doc1 vs doc2 = 14000

  doc1 vs doc3 = 1000

  doc1 vs doc4 = 11000

• Similaridade do cosseno: doc1 vs doc2 = 1.0

  doc1 vs doc3 = 0.71

  doc1 vs doc4 = 0.78

O produto escalar privilegia vetores de maior magnitude, enquanto a similaridade do cosseno destaca a proporção entre os componentes (direção).

Compreendendo cos(θ) nas métricas

O ângulo θ representa simplesmente o ângulo entre os vetores. O valor do cosseno é uma forma conveniente de medir essa relação, variando entre -1 e 1. Para obter o ângulo real em graus ou radianos, basta utilizar a função arco-cosseno.

import torch
import torch.nn.functional as F
import math

A = torch.tensor([1.5, 1.5])
B = torch.tensor([2.0, 1.0])
cos = F.cosine_similarity(A, B, dim=0)
theta = math.acos(cos)
theta_degrees = math.degrees(theta)

Distância de Manhattan (L1) e Distância Euclidiana (L2)

• Distância de Manhattan: Soma das diferenças absolutas de cada dimensão.
• Distância Euclidiana: Distância em linha reta entre os pontos.

A Manhattan é interessante para trajetos em “grade” (como ruas de uma cidade), ou quando as dimensões possuem relevância diferente; já a Euclidiana é indicada para medir a distância direta, quando todas as variáveis são igualmente importantes. Em geral, a Manhattan resulta em valores maiores; e, em espaços de alta dimensão, pode ser preferível [2]

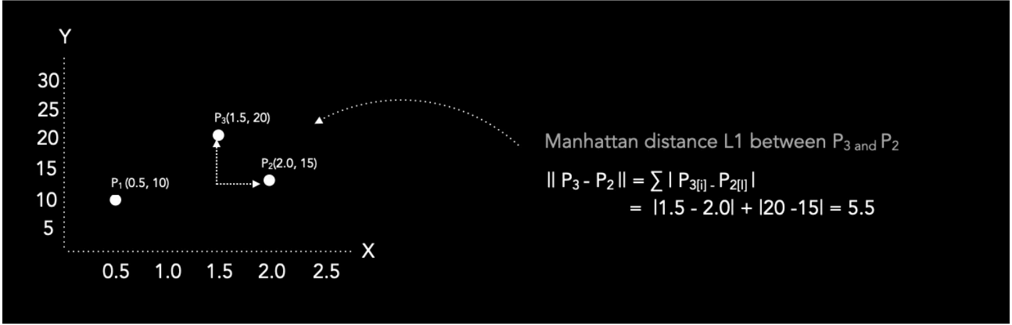Figura: Distância de Manhattan

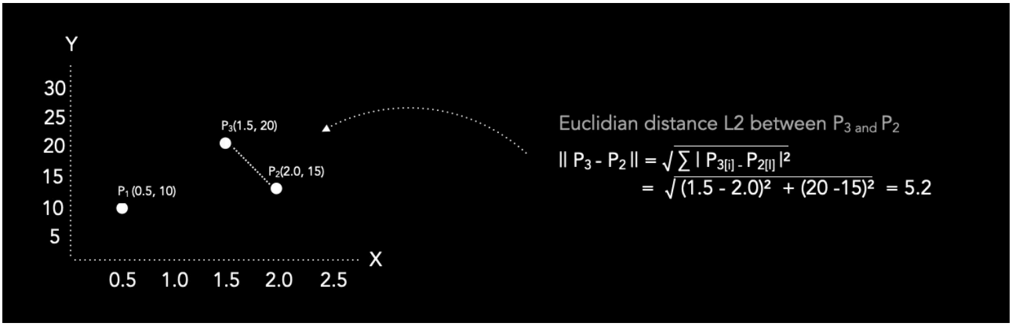Figura: Distância Euclidiana

Comparando Vetores de Dimensões Diferentes

Comparações só fazem sentido entre vetores de mesma dimensão, pois cada dimensão representa uma característica específica. Caso contrário, é necessário padronizar os vetores menores adicionando zeros nas dimensões faltantes.

Referências

[1] Khan Academy, “Dot products – Multivariable Calculus”, 2025. https://pt.khanacademy.org/math/multivariable-calculus/dot-products

[2] C. Aggarwal, A. Hinneburg e D. Keim, “On the Surprising Behavior of Distance Metrics in High Dimensional Space”, 2001. https://bib.dbvis.de/uploadedFiles/155.pdf